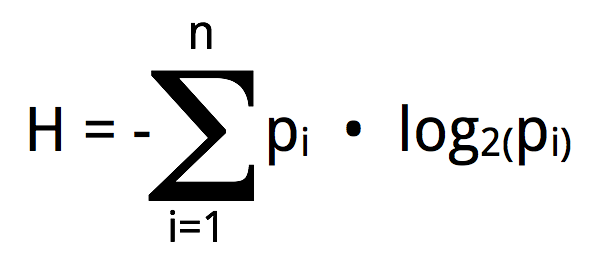Before we start, please be sure to download ITdojo’s password entropy worksheet (MS Excel, OS X Numbers, LibreOffice Calc compatible). It’s a nice companion to this post and a useful tool later down the road.
It’s mandated by policy. It’s a best practice for sure. And it’s nothing new to virtually all of us: Passwords are supposed to be long, varied in their use of characters (upper case, lower case, numbers, special characters) and not based on dictionary words. Simple enough, right? But let me push a little further and ask a not-so-simple question:
Which is stronger, an 8-character, random password that potentially uses characters from the entire ASCII characters set (upper-case, lower-case, numbers, special characters (including a space)) or a 10-character, random password that uses only upper and lower-case letters?
Please disregard for a moment whether you feel either of them is sufficiently strong for your situation; that’s another discussion.
How can you make an apples-to-apples comparison of the two passwords? They differ in many ways. One argument may state that a longer password, even when using a smaller potential character set is stronger. Another argument might assert that the shorter password has the potential to be stronger because it pulls from a larger list of potential characters. One argument is for length, the other is for complexity. So which is more resistant to attack?
This question lends itself directly to discussions of policy within an organization. How can we compare the potential strength of any proposed password policy? Are your policy requirements arbitrary or based on some sort of quantitative measure? It’s simple to say, ‘make passwords long, complex and not based on dictionary words’, but can you quantify what ‘enough’ is for a given situation? Scenarios vary. We all have different needs and systems have varying levels of password support. Moreso, is there a point of diminishing returns on password complexity? At what point do they become so long and complex that they become practically unusable? Again, there is no textbook answer here. But for you and your shop, there is an answer.
The answer to these questions lies in password entropy (part of it, at least). Volumes of discussion can be had on concepts of information entropy and its uses in communication but for our purposes today let’s just say that, in the end, password entropy provides us a way of empirically comparing the potential strength of a password based upon its length and the potential number of characters it might contain. To explain why, let me start with a simple demonstration.
Please randomly select a letter from A – Z.
I will now attempt to guess it. How many guesses do you think it will take me? Do you think its random, based on luck? Could I guess it in one try? Sure. But it could also take me 25 guesses, right? If I were to just randomly start guessing my success would be random, too. But if I apply basic concepts from Claude Shannon’s information theory to the task, something very interesting happens. No matter which letter you select it will always take me as few as four (4) but never more than five (5) questions to guess your letter. In contrast, if I were to guess at random it would, on average, take me 13 guesses to guess your letter. But when concepts of information entropy are applied, the number of questions/guesses drops to a consistent 4 or 5. The reason why is fairly simple: I don’t guess letters; I eliminate them. Let’s suppose that the letter you selected is “D“. Here is how my questioning will go:
- Question #1: Is your letter between N and Z? Your answer: No.
- If Yes, your letter is between N-Z.
- If No, your letter is between A-M.
- Question 2: Is your letter between A and G? Your answer: Yes.
- If Yes, your letter is between A-G.
- If No, your letter is between H-M.
- Question 3: Is your letter between A-D? Your answer: Yes.
- If Yes, your letter is between A-D.
- If No, your letter is between E-G.
- Question 4: Is your letter between A-B? Your answer: No.
- If Yes, your letter is between A-B.
- If No, your letter is between C-D.
- Question 5: Is your letter C? Your answer: No.
- If Yes, your letter is C.
- If No, you letter is D.
Result: Your letter is D. Guesses: 5
Let’s do that again. This time let’s assume you randomly choose the letter “H“.
- Question #1: Is your letter between N and Z? Your answer: No.
- If Yes, your letter is between N-Z.
- If No, your letter is between A-M.
- Question 2: Is your letter between A and G? Your answer: No.
- If Yes, your letter is between A-G.
- If No, your letter is between H-M.
- Question 3: Is your letter between H-I? Your answer: Yes.
- If Yes, your letter is between H-I.
- If No, your letter is between J-K.
- Question 4: Is your letter H? Your answer: Yes.
- If Yes, your letter is H.
- If No, your letter is between I-J.
Result: Your letter is H. Guesses: 4
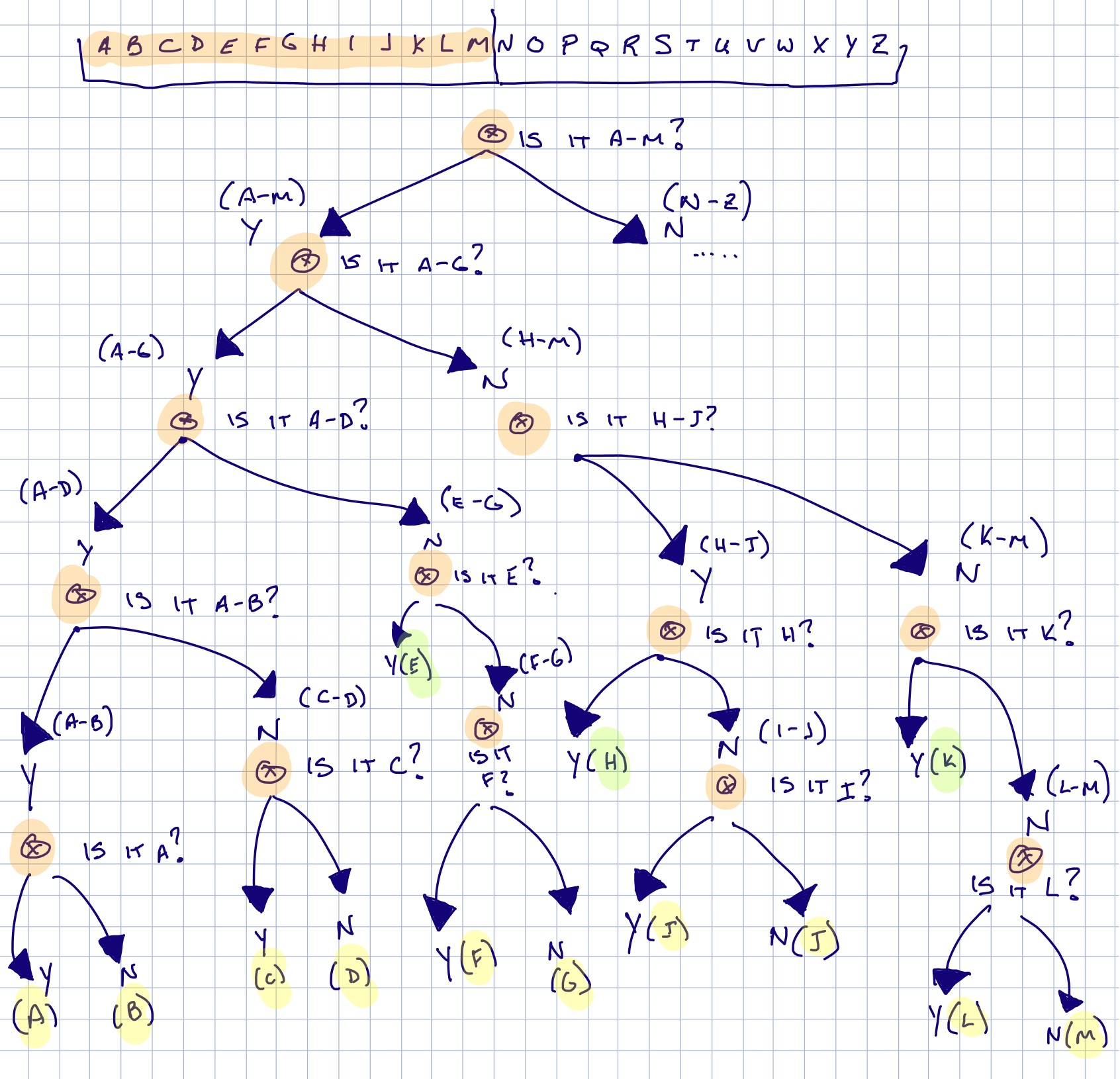
The image below shows my decision tree. Each orange ‘x’ is a question. The green highlighted letters can be identified in 4 questions and the yellow highlighted letters will be identified in 5. The decision tree in the image only shows the left-half of the alphabet (A-M). You can replicate the right side of the alphabet (N-Z) into a similar looking tree. If you examine the number of questions for all 26 letters in the alphabet you will find that six (6) of the letters can be identified in four (4) questions while the remaining twenty (20) letters will be identified in five (5) questions.
So, if we were to play this guessing game over and over, how many guesses, on average, would it take me to guess your letter?
To calculate the average number of questions I will have to ask to determine your letter I have to know what the probability of a letter being selected will be. For this example I am assuming that each of the 26 letters in the alphabet has a statistically equal chance of being selected by you (more on the nuance of this assumption later). Quick math shows that 1/26 = 0.0384. Convert that into a percentage and we learn that each letter has a 3.84% chance of being the letter you randomly selected.
At the risk of boring you with some math, there is an equation that will answer the question. It is:
This equation calculates H, which is the symbol used for entropy. For our alphabet the equation would end up looking like this:
H = -[(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+
(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+
(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+
(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+
(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+(0.038log2•0.038)+
(0.038log2•0.038)+(0.038log2•0.038)] = 4.7004And now we have the answer: I will have to ask an AVERAGE of 4.7004 questions to determine your randomly selected letter from the alphabet.
More formally, we would say that there are 4.7004 ‘bits of entropy’.
If you apply this math to a single character randomly selected from the following character sets you will get the following:
- Binary (0, 1) –> H = 1 (1 bit of entropy)
- I will have to ask one question to determine if your randomly selected value is a 1 or a 0.
- Decimal (0-9) –> H = 3.32193 (3.2193 bits of entropy)
- I will have to ask an average of 3.32193 questions to determine your randomly selected number (0-9).
- Hexadecimal (0-9, A-F) –> H = 4.000
- I will have to ask four (4) questions to determine your value (a-f, 0-9)
- Upper & lower case alphabet (a-z, A-Z) –> H = 5.7004
- I will have to ask an average of 5.7004 questions to determine your randomly selected letter (a-z, A-Z).
- All printable ASCII characters (including space) –> H = 6.5699
- I will have to ask an average of 6.5699 questions to determine your randomly selected value.
Now, let’s build on this a little bit more. The numbers above are for a SINGLE letter you randomly selected. What if I were to ask you to choose two (2) letters randomly. Now, guessing one letter at a time, how many guesses, on average, would it take me to discover both of them? The answer is additive, meaning you need only add the entropy for each letter. If the entropy of a single lower-case letter is 4.7004, the entropy of two randomly selected letters is 4.7004 + 4.7004. That’s 9.4008 questions to determine both letters (assuming a-z, as in our original example). If I were to ask you to select a string of ten (10) random characters it will require an average of 47.004 questions (4.7004 * 10) to guess them all.
This is all well and good but it assumes that I am able to guess each value one at a time. If you were to pick 10 letters randomly from the alphabet I could guess the first one in about 4.7 guesses, the second in 4.7 guesses, the third in 4.7 guesses and so on. But guessing passwords is not done one character at a time (we hope). An attacker will have to correctly guess all ten values at once in order to determine the randomly selected letters. This is, obviously, a much more difficult thing to do. But how difficult? To find out let’s circle back around to the original question I asked:
[box icon=”question-sign” style=”simple”]Which is stronger, an 8-character, random password that potentially uses characters from the entire ASCII characters set (upper-case, lower-case, numbers, special characters (including a space)) or a 10-character, random password that uses only upper and lower-case letters?[/box]
Well, if your character set is 26 lower-case letters (a-z), 26 upper-case characters (A-Z), and your password is 10 characters long there will be 5210 possible combinations of letters (26 characters (a-z) + 26 characters (A-Z) = 52 characters). That’s a big number. 144,555,105,949,057,000 (144.5 quadrillion), to be exact..
So, to summarize those values:
- Number of characters in character set (a-z, A-Z): 52
- Number of characters in password: 10
- Total number of possible combinations of 10-character strings: = 5210 = 144,555,105,949,057,000
Here’s where the magic kicks in:
What is the entropy of a single character in the full alpha character set (a-z, A-Z)? We already determined this to be 5.7004.
How long is your randomly selected string of characters? 10-characters.
What is the entropy of a 10-character string using the upper/lower-case alpha characters set? 5.7004 * 10 = 57.004
What is 257.004 ? It’s 144,555,105,949,057,000!!! Holy smokes!!! It’s the same number as 5210 !!!
Your 10-character, upper/lower-case string (password) has 57.004 bits of entropy. Assuming an attacker would guess the string in 50% of all possible guesses we estimate he/she will have to make 72,277,552,974,528,300 guesses (yes, on average) before guessing your 10-characters string.
To say this in a more meaningful way: A 10-character upper/lower-case password has 57.004 bits of entropy.
So how many bits of entropy does our competing password have? It is an 8-character password that utilizes the full printable ASCII character set (including a space). If you refer back to the middle of this post you’ll see that a character randomly selected from the full printable ASCII characters set has 6.5699 bits of entropy. This means that an 8-character password randomly selected from that range will have 52.559 (8 * 6.5699) bits of entropy.
To summarize the 8-characters passwords values:
Number of characters in character set (a-z, A-Z, 0-9, all special characters, incl. space): 95
Number of characters in password: 8
Total number of possible combinations of 8-character strings: = 958 = 6,634,204,312,890,620 (6.63 quadrillion)
And we see that the magic is real:
What is the entropy of a single character in the full printable ASCII character set (including space)? We already determined this to be 6.5699.
How long is your randomly selected string of characters? 8-characters.
What is the entropy of a 8-character string using the upper & lower-case alpha characters set? 6.5699 * 8 = 52.559
What is 252.559 ? It’s 6,634,204,312,890,620!!! Holy smokes again!!! It’s the same number as 958 !!!
- Our 10-character, upper/lower-case password has 57.004 bits of entropy.
- Our 8-character, full ASCII character-set password has 52.559 bits of entropy.
The more bits of entropy a password has the stronger it is. And, this is important, a single bit of entropy represents an EXPONENTIAL increase in strength. There is a hug difference between the strength of our two passwords (4.445 orders of magnitude); that’s not trivial. It’s massive.
So why use entropy as an expression of password strength? Information theory gurus can probably lecture for days on such questions but I have one simple answer: humans really suck at dealing with large numbers. Just look at how we express phone numbers, IP addresses, credit card numbers and social security numbers for evidence of our big-number loathing. If there is a way to simplify the expression of a value, let’s do so. After all, what is easier to say and understand?:
- My password has 5210 possibilities or 958 possibilities.
or; - My password has 57.004 bits of entropy vs 52.559 bits of entropy.
Hopefully, you will find the latter more agreeable.
The greater the number of bits of entropy a password has the stronger it has the potential to be. I use the word ‘potential’ here because there are many nuances to this discussion that can make these numbers an inaccurate reflection of password strength. At the top of the list is the fact that most passwords are generated by humans, not by random number generators. Humans are really, really bad at generating randomness. Seriously. We’re terrible at it. This means that the equation used above, which assumes that each character has an equal likelihood of being selected is not going to be as accurate when a person is picking the letters. When attackers can start making really good guesses about how passwords are being created (allowing them to exclude certain values, for example) the entropy can drop very quickly. This is bad.
One of your organization’s systems may support the use of the full ASCII character set when setting passwords while another may only support alphanumeric passwords. How many bits of entropy should a password have in order to be adequately secure? How long does an alphanumeric password have to be in order to be as strong as a password that uses the full character set? That’s a really important question to be able to answer, especially when it comes to a policy on passwords. Specifying password length may be an inadequate measure of strength; specifying password entropy requirements has the potential to be a much more consistent expression of security requirements. Alas, there is no textbook definition here but a lot of organizations like to see 80-bits of entropy or more. For now, that’s a lot of entropy. Check back in a few years and we may see that such a statement has become untrue (Moore’s Law). If you play around with the spreadsheet linked at the beginning of this post you can gain some good insight in just how much entropy your password schemes will have. Note: In the spreadsheet, the orange fields are editable. Disable protection in the spreadsheet if you need to tinker with the other values.
One final note: there are a lot of variables that should be discussed when exploring passwords. Complexity, length and entropy are all great items to understand but other factors can be just as important. What underlying mechanisms do your passwords employ? What hashing algorithm? Are passwords salted? Does your system utilize key stretching techniques? Are any type of backward compatibility mechanisms enabled (NTLM, etc.)? These things factor into the discussion just as much as entropy and can have a big impact on just how much effort an attacker will have to put forth to guess the password. It’s a big topic, worthy of a lot of thoughtful contemplation and discussion. Entropy is a great place to start …it’s just not the only thing to consider.
Cheers,
Colin
If you liked this post, please consider sharing it. Thanks!